En las Artes liberales, la Geometría es la ciencia que estudia las Leyes o principios matemáticos que nos permite medir a un nivel interior la creación manifestada. También Geometría equivale a “Diva Mater “(Madre tierra) o como ya la conocemos en este espacio…Gea, esposa de Urano y madre de los Titanes. SELECCIONES

Pitágoras y la escuela pitagórica es un claro ejemplo de las artes liberales y como éstas pueden ser utilizadas para transmitir más de lo que transmiten. Como en la música podemos encontrar una buena analogía de las octavas, en la matemática también podemos encontrar no sólo analogías o una herramienta práctica, sino también un manual esotérico y filosófico de los mejores y más completos. Si bien éste no era un tema programado, la tabla de Helimer merece un ejemplo claro de las artes liberales, por ese motivo me centraré hoy en cómo podemos desvelar conocimiento de un simple teorema pitagórico que todos conocemos y hemos visto alguna vez en nuestros estudios y aprendizaje.

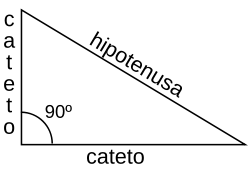
Las matemáticas se dividen en tres grandes ramas, una triada compuesta por la Aritmética, el Algebra y la Geometría, que corresponden al pensamiento (Aritmética), palabra (Algebra) y obra (Geometría). De esta triada tomaremos la Geometría y nos centraremos en el conocido teorema de Pitágoras. Este dice que el cuadrado de los catetos de un triángulo rectángulo es igual al cuadrado de su hipotenusa. Se llama triángulo rectángulo a aquel triángulo que tiene un ángulo recto de 90º. Los lados que comparten ese ángulo recto se llaman catetos, y el lado que une los extremos se llama hipotenusa (ver imagen). Tenemos entonces un triángulo formado por tres lados (a, b y c) donde (a) y (b) son catetos y (c) hipotenusa. Ahora volvamos a la definición del teorema

“La suma del cuadrado de los catetos de un triángulo rectángulo, es igual al cuadrado de su hipotenusa”

Si desarrollamos este enunciado, su fórmula algebraica (palabra) sería: a² + b² = c² donde los cuadrados representan superficie. Veamos ahora la figura geométrica (obra) del teorema de Pitágoras y su funcionamiento

Como pueden apreciar en la imagen giff de arriba, es algo más que conocido. Seguramente todos aquellos que lo han estudiado, alguna vez se han preguntado ¿para qué sirve esto?, pues en lo práctico del hombre común, sólo a determinados profesionales como topógrafos, ingenieros, arquitectos y demás profesiones de las ciencias exactas le son de utilidad, pero para el resto de la gente, sólo es información cultural sin un uso práctico o necesario alguno. Pues veremos ahora lo que oculta el teorema y observarán que hay mucho más escondido a los ojos del neófito, pero visible a los ojos del iniciado. pues así ocultaba Pitágoras su conocimiento y sabiduría para ser transmitida solo a sus discípulos.

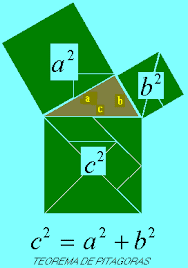
Como primera observación vemos que el teorema en sí, es un ejemplo de dualidad, pues sus componentes se multiplican por si mismos al elevarse al cuadrado (a² + b² = c²). Luego confirma que la suma de las partes (a² + b²) hacen al todo (c²) y por último describe una triada, pues el teorema está formado por tres componentes (a, b y c) en toda su forma. Ahora avancemos un poco más, y trabajemos con la geometría. Tomando como parámetro la superficie de los cuadrados A y B, vemos que el teorema nos dice que su sumatoria da como resultado otra superficie. Llevemos esto a lo que ya conocemos, y reemplacemos superficie (espacio) por espacio matricial. Si (a)² es igual a A, (b)² es igual a B y (c)² es igual a C, tendríamos que la sumatoria de A y B daría C donde A, B y C son espacios matriciales. Veamos ahora en la práctica como resolver esto

(a)² = A, donde (a) = 4 y A = 16

(b)² = B, donde (b) = 3 y B = 9

(c)² = C, donde (c) = 5 y C = 25

(EM4x4) + (EM3x3) = EM5x5 => 16 + 9 = 25

Podemos postular. siguiendo esta lógica, que la sumatoria de dos espacios matriciales dan como resultado otro espacio matricial cuyas realidades son la sumatoria de realidades de los espacios matriciales sumados. Ahora demos un paso más en el análisis del teorema y sustituyamos los espacios matriciales por el tiempo, ya que el tiempo es espacio por manifestarse o ya manifestado.

Tendríamos un tiempo uno al cuadrado (t1)², más un tiempo dos al cuadrado (t2)², dando como resultado un tiempo tres al cuadrado (t3)², siendo entonces una ecuación de la siguiente fórmula: (t1)² + (t2)² = (t3)². Si (t1) y (t2) son distintos momentos de una octava, (t3) resulta de la sumatoria de esos momentos, siendo entonces la fórmula matemática del tiempo lineal donde un tiempo al cuadrado (espacio) más otro tiempo al cuadrado (espacio) da como resultado un tercer tiempo al cuadrado (espacio) que contiene a los dos tiempos anteriores. En palabras claras, el presente contiene al pasado como el futuro al presente y el pasado al futuro, una octava proyectiva en toda su regla.

Bueno, podríamos seguir por un largo tiempo más analizando y hablando de lo que oculta el teorema de Pitágoras, pero creo que hasta aquí es suficiente, pues entrar en más profundidad requeriría de extensas introducciones que ahora no estoy dispuesto a afrontar, sepan disculpar mi poca voluntad al respecto. Para finalizar decir que todas las matemáticas como expresión de la creación, tienes información, conocimiento y sabiduría que develar.

“Una flor es la expresión matemática de la belleza, es como la naturaleza se comunica con nosotros mostrándonos en sus hermosas formas y colores, los fractales de la creación, permitiéndonos medir a un nivel interior, la creación manifestada ” (a² + b² = c²)